「タンジェント・フラクション」問題
締め切りが 2017/06/15 10:00 AM なので,その 1 分後に投稿されるように予約
設問
α と β を、0 < α < β < π/2 を満たす実数とします。
α, β の組のうち、tan(α), tan(β), tan(α+β) がすべて単位分数(分母が自然数、分子が 1 の分数として書き表せる数)となるものを考えましょう。(α, β の単位はラジアンと見なします。)
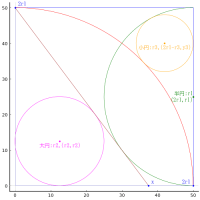
例えば下図の青色の正方形の格子において、図のように α(≒0.3218)と β(≒0.4636)をとると、tan(α)=1/3, tan(β)=1/2 です。
さらに黒色の三角形が直角二等辺三角形となるため、tan(α+β)=1 となり、このような α と β が題意を満たすことが分かります。

正の実数 m に対し、m ≦ α+β の範囲で題意を満たす α, β の組の個数を F(m) と定義します。
例えば F(0.5)=1,F(0.3)=4,F(0.1)=15,F(0.01)=266 となることが確かめられます。
標準入力から、正の実数 m(0.001 < m < 1)が与えられます。
標準出力に F(m) の値を出力するプログラムを書いてください。
なお入力値の小数点以下の桁数は最大で 4 桁とします。
=====================================
tan(α+β) = (tan α + tan β) / (1-tan α tan β)
tan α = 1/a, tan β = 1/b なる a, b を用いて,
tan(α+β) = (1/a+1/b) /(1-(1/a)(1/b)) = (a+b) / (ab-1)
tan(α+β) が単位分数であるためには ab-1 が a+b で割り切れればよい。
よって,問題は 整数 a, b で ab-1 が a+b で割り切れる組み合わせを数えればよい。
ただし,1/a + 1/b > m であること 1/a + 1/b < π/2 という条件の下で。
出題の範囲では,1≦ a, b ≦ 10^6 で探索すればよいが,枝刈りが必須。
第一次解
F = function(m) {
max = 1e+06
count = 0
for (a in 2:(2/m)) {
limit = m - 1/a
for (b in a:max) {
if (b * limit >= 1) {
break
}
abm1 = a * b - 1
apb = a + b
if (abm1%%apb == 0) {
count = count + 1
}
}
}
cat(count)
}
system.time(F(0.6)) # 1, 0.015 sec.
system.time(F(0.5)) # 1, 0.304 sec.
system.time(F(0.3)) # 4, 0.548 sec.
system.time(F(0.1)) # 15, 2.478 sec.
system.time(F(0.02)) # 117, 13.545 sec.
system.time(F(0.012)) # 219, 22.501 sec.
system.time(F(0.01)) # 266, 26.629 sec.
system.time(F(0.0098)) # 272, 29.057 sec.
system.time(F(0.0048)) # 628, 55.406 sec.
system.time(F(0.0013)) # 2791, 205.393 sec.
system.time(F(0.0011)) # 3382, 244.198 sec.
時間が掛かりすぎる。
第二次解
F = function(m) {
count = 0
for (a in 2:(2/m)) {
b = a:1e+06 # 内側の for をなくす
b = b[1 > b * (m-1/a)]
count = count + sum((a * b - 1) %% (a + b) == 0)
}
cat(count)
}
system.time(F(0.6)) # 1, 0.027 sec.
system.time(F(0.5)) # 1, 0.048 sec.
system.time(F(0.3)) # 4, 0.089 sec.
system.time(F(0.1)) # 15, 0.448 sec.
system.time(F(0.02)) # 117, 2.336 sec.
system.time(F(0.012)) # 219, 3.880 sec.
system.time(F(0.01)) # 266, 4.738 sec.
system.time(F(0.0098)) # 272, 4.909 sec.
system.time(F(0.0048)) # 628, 10.261 sec.
system.time(F(0.0013)) # 2791, 38.881 sec.
system.time(F(0.0011)) # 3382, 45.998 sec.
第三次解
F = function(m) {
max = 1e+06
count = 0
for (a in 2:(2/m)) {
b = a:min(max-1, a * (a - 1) + 1) # 範囲を絞る
b = b[1 > b * (m - 1/a)]
count = count+sum((a * b - 1) %% (a + b) == 0)
}
cat(count)
}
system.time(F(0.6)) # 1, 0 sec.
system.time(F(0.5)) # 1, 0 sec.
system.time(F(0.3)) # 4, 0 sec.
system.time(F(0.1)) # 15, 0 sec.
system.time(F(0.02)) # 117, 0.004 sec.
system.time(F(0.012)) # 219, 0.017 sec.
system.time(F(0.01)) # 266, 0.028 sec.
system.time(F(0.0098)) # 272, 0.029 sec.
system.time(F(0.0048)) # 628, 0.297 sec.
system.time(F(0.0013)) # 2791, 12.958 sec.
system.time(F(0.0011)) # 3382, 18.321 sec.
最終解 爆速
F = function(m) {
max = 1e+06
count = 0
for (a in 2:(2/m)) {
b = as.integer((a*(a-1:a)+1) / 1:a) # 大幅に絞る
b = b[b >= a]
b = b[1 > b*(m-1/a)]
count = count+sum((a * b - 1) %% (a+b) == 0)
}
cat(count)
}
system.time(F(0.6)) # 1, 0 sec.
system.time(F(0.5)) # 1, 0 sec.
system.time(F(0.3)) # 4, 0 sec.
system.time(F(0.1)) # 15, 0 sec.
system.time(F(0.02)) # 117, 0 sec.
system.time(F(0.012)) # 219, 0.001 sec.
system.time(F(0.01)) # 266, 0.002 sec.
system.time(F(0.0098)) # 272, 0.002 sec.
system.time(F(0.0048)) # 628, 0.004 sec.
system.time(F(0.0013)) # 2791, 0.084 sec.
system.time(F(0.0011)) # 3382, 0.070 sec.