こんにちは。東久留米市の学習塾塾長です。
今回は、2018年開成中入試に出題された面積問題を取り上げます。
問題は、
「下の図において、四角形ABCDは正方形で、BE=EF=FC、CG=GDです。
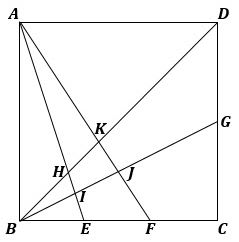
▲問題図
(i) 三角形AIJと四角形ABCDの面積比を最も簡単な整数の比で答えなさい。
(ii) 四角形HIJKと四角形ABCDの面積比を最も簡単な整数の比で答えなさい。」
です。
早速、取り掛かりましょう。
図1のように、GからDAに平行な直線を引き、それとAB、AE、AF、BDとの交点をそれぞれL、S、R、Qとし、さらに、H、I、K、JからBCに下ろした垂線の足をそれぞれM、N、O、Pとします。
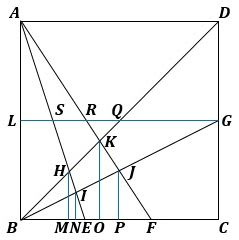
▲図1.L、S、R、Q、M、N、O、Pを置きました
(i)から始めましょう。
図2のように、△ABEに着目すると、△ABE∽△ALSで、その相似比は2:1です。

▲図2.△ABE∽△ALSで、その相似比は2:1です
ここで、正方形ABCDの一辺の長さを1とすると、BE=1/3なので、LS=1/6で、したがって、GS=5/6 になります。
そこで図3のように△IBEと△IGSに着目すると、それらは相似で、その相似比は、1/3:5/6=2:5です。
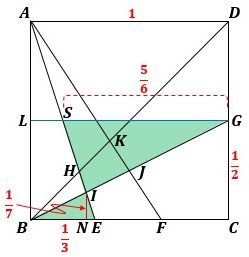
▲図3.△IBE∽△IGSで、その相似比は2:5です
したがって、IN=1/7 になります。
続いて図4のように、△ABFに着目すると、△ABF∽△ALRで、その相似比は2:1です。
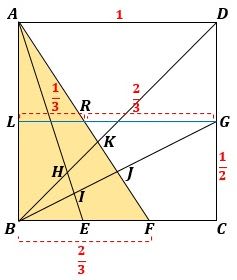
▲図4.△ABF∽△ALRで、その相似比は2:1です
このとき、BF=2/3なので、LR=1/3で、GR=2/3 になります。
そこで図5のように△JBFと△JGRに着目すると、それらは相似で、その相似比は、2/3:2/3=1:1です。
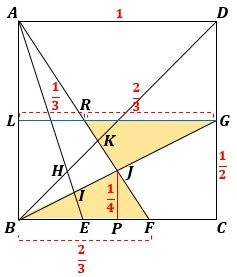
▲図5.△JBF∽△JGRで、その相似比は1:1です
したがって、JP=1/4 になります。
ここから△AIJの面積S(△AIJ)を計算しましょう。
S(△AIJ)=S(△AEF)-S(△JBF)+S(△IBE)
で、
S(△AEF)=1/3×1×1/2=1/6
S(△JBF)=2/3×1/4×1/2=1/12
S(△IBE)=1/3×1/7×1/2=1/42
から、
S(△AIJ)=1/6-1/12+1/42
=(14-7+2)/84
=9/84
=3/28
です。
ここで、正方形ABCDの面積は1なので、三角形AIJと四角形ABCDの面積比は、3/28:1= 3:28 で、これが答えです。
続いて(ii)です。
図6のように、△HBEと△HQSに着目すると、それらは相似です。

▲図6.△HBE∽△HQSで、その相似比は1:1です
このとき、SQ=LQ-LS=1/2-1/6=1/3なので、△HBEと△HQSの相似比は1:1 になり、HM=1/4です。
一方、JP=1/4ですから、HM=JPで、HJはBC、LGに平行になります。
すると△AEFと△AHJは相似で、図7のように、その相似比は1:3/4=4:3です。

▲図7.△AEF∽△AHJで、その相似比は4:3です
したがって、HJ=1/4 になります。
次に図8のように、△KBFと△KQRに着目すると、それらは相似で、その相似比は2/3:1/6=4:1です。
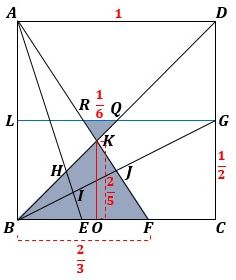
▲図8.△KBF∽△KQRで、その相似比は4:1です
したがって、KO=2/5 になります。
ここから四角形HIJKの面積S(□HIJK)を計算しましょう。
S(□HIJK)=S(△KHJ)+S(△IHJ)
で、
S(△KHJ)=HJ×(KO-HM)×1/2=1/4×(2/5-1/4)×1/2=1/8×3/20=3/32×1/5
S(△IHJ)=HJ×(HM-IN)×1/2=1/4×(1/4-1/7)×1/2=1/8×3/28=3/32×1/7
から、
S(□HIJK)=3/32×1/5+3/32×1/7
=3/32×(1/5+1/7)
=3/32×12/35
=9/280
です。
したがって、四角形HIJKと四角形ABCDの面積比は、9/280:1= 3:280 で、これが答えです。
見通しのよい問題です。
今回は、2018年開成中入試に出題された面積問題を取り上げます。
問題は、
「下の図において、四角形ABCDは正方形で、BE=EF=FC、CG=GDです。

▲問題図
(i) 三角形AIJと四角形ABCDの面積比を最も簡単な整数の比で答えなさい。
(ii) 四角形HIJKと四角形ABCDの面積比を最も簡単な整数の比で答えなさい。」
です。
早速、取り掛かりましょう。
図1のように、GからDAに平行な直線を引き、それとAB、AE、AF、BDとの交点をそれぞれL、S、R、Qとし、さらに、H、I、K、JからBCに下ろした垂線の足をそれぞれM、N、O、Pとします。

▲図1.L、S、R、Q、M、N、O、Pを置きました
(i)から始めましょう。
図2のように、△ABEに着目すると、△ABE∽△ALSで、その相似比は2:1です。

▲図2.△ABE∽△ALSで、その相似比は2:1です
ここで、正方形ABCDの一辺の長さを1とすると、BE=1/3なので、LS=1/6で、したがって、GS=5/6 になります。
そこで図3のように△IBEと△IGSに着目すると、それらは相似で、その相似比は、1/3:5/6=2:5です。

▲図3.△IBE∽△IGSで、その相似比は2:5です
したがって、IN=1/7 になります。
続いて図4のように、△ABFに着目すると、△ABF∽△ALRで、その相似比は2:1です。

▲図4.△ABF∽△ALRで、その相似比は2:1です
このとき、BF=2/3なので、LR=1/3で、GR=2/3 になります。
そこで図5のように△JBFと△JGRに着目すると、それらは相似で、その相似比は、2/3:2/3=1:1です。

▲図5.△JBF∽△JGRで、その相似比は1:1です
したがって、JP=1/4 になります。
ここから△AIJの面積S(△AIJ)を計算しましょう。
S(△AIJ)=S(△AEF)-S(△JBF)+S(△IBE)
で、
S(△AEF)=1/3×1×1/2=1/6
S(△JBF)=2/3×1/4×1/2=1/12
S(△IBE)=1/3×1/7×1/2=1/42
から、
S(△AIJ)=1/6-1/12+1/42
=(14-7+2)/84
=9/84
=3/28
です。
ここで、正方形ABCDの面積は1なので、三角形AIJと四角形ABCDの面積比は、3/28:1= 3:28 で、これが答えです。
続いて(ii)です。
図6のように、△HBEと△HQSに着目すると、それらは相似です。

▲図6.△HBE∽△HQSで、その相似比は1:1です
このとき、SQ=LQ-LS=1/2-1/6=1/3なので、△HBEと△HQSの相似比は1:1 になり、HM=1/4です。
一方、JP=1/4ですから、HM=JPで、HJはBC、LGに平行になります。
すると△AEFと△AHJは相似で、図7のように、その相似比は1:3/4=4:3です。

▲図7.△AEF∽△AHJで、その相似比は4:3です
したがって、HJ=1/4 になります。
次に図8のように、△KBFと△KQRに着目すると、それらは相似で、その相似比は2/3:1/6=4:1です。

▲図8.△KBF∽△KQRで、その相似比は4:1です
したがって、KO=2/5 になります。
ここから四角形HIJKの面積S(□HIJK)を計算しましょう。
S(□HIJK)=S(△KHJ)+S(△IHJ)
で、
S(△KHJ)=HJ×(KO-HM)×1/2=1/4×(2/5-1/4)×1/2=1/8×3/20=3/32×1/5
S(△IHJ)=HJ×(HM-IN)×1/2=1/4×(1/4-1/7)×1/2=1/8×3/28=3/32×1/7
から、
S(□HIJK)=3/32×1/5+3/32×1/7
=3/32×(1/5+1/7)
=3/32×12/35
=9/280
です。
したがって、四角形HIJKと四角形ABCDの面積比は、9/280:1= 3:280 で、これが答えです。
見通しのよい問題です。




















