シュバルツシルト解における時空の距離 ds2は、以下の通り。
ds2 = -(β・c・dt)2 + ((1/β)・dx)2・・・・⑧
シュバルツシルト解の初期条件(境界条件)で、時空の歪は星の中心から球対象であるとしたので、半径方向を x 軸にとり、y軸と、z軸は 0 とした。
β: 質量 M の星の中心から半径 r の位置の時空の歪で、以下の通り。
β= √(1 - 2GM/(c2・r))・・・・⑨
G: 万有引力定数
c: 光速度
dx: 星の中心を 0 とした場合の半径 r 方向の座標
下図のように、質量 M の星から半径 r の位置で質量 m のロケットが自由落下しているとする。
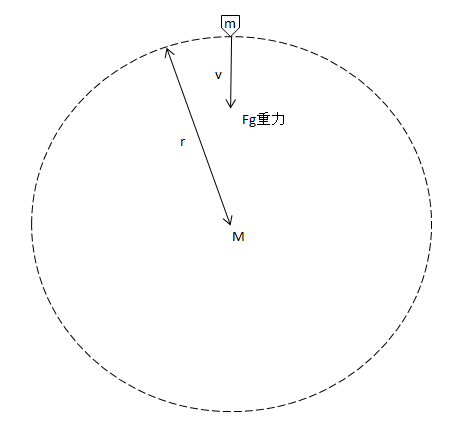
このロケットの半径 r の位置での落下速度を v とすると、ロケットの運動エネルギー Ekは、
Ek = (1/2)mv2・・・・⑩
となる。
ロケットに働く重力を Fg とすると、
ニュートンの万有引力の法則より、
Fg = GMm/r2・・・・⑪
重力Fgを半径 r で積分すると、距離 r でのポテンシャルエネルギー Epは、
Ep = - GMm /r + C0・・・・⑫
となる。
C0は、積分定数
r = ∞ の場合、Ep = C0 となるので、
無限遠でのポテンシャルエネルギー Ep が 0 だとすると、積分定数 C0 = 0 となり、
ポテンシャルエネルギーEpは、
Ep = - GMm/r・・・・⑬
となる。
ロケットは無限遠で v = 0 で運動エネルギー Ep = 0、ポテンシャルエネルギー Ep = 0 の状態から、質量 M の星に向かって自由落下したとすると、
エネルギーの保存則より、
Ep + Ek = 0
式⑬と、式⑩より、
- GMm/r + (1/2)m・v2 = 0
v2 = 2GM/r・・・・⑭となる。
式⑭にはロケットの質量 m が含まれないので、質量 m に関係なく成立する。
無限遠の観測者の時刻を T、ロケット内部での時刻を T' とすると、特殊相対性理論のローレンツ縮小により、ロケットの時刻は β の割合で遅れる。
T' = β・T
たとえば、β = 0.1 だとすると、無限遠の観測者の時刻 T で 10 年経過しても、ロケット内部の時刻 T' では、1年しか経過していないことになる。
ローレンツ収縮より、
β = √( 1 - v2 / c2)・・・・⑮
式⑮に、式⑬を代入すると、
β= √(1 - 2GM/(c2・r))
となり、式⑨が得られる。
ここまでは、割とあっさりと時空の歪βが求められた。
ところが、不思議なのは、「一般相対性理論と等価原理、重力による時間と長さの収縮と非ユーグリッド座標系 」で遠心力と、重力が釣り合うことから時空の歪みβを求めた際には、
β = √(1 - gr/c2)・・・・⑮
が得られた。
式⑯にニュートンの万有引力の法則より、
g = GM/r2
を代入すると
β= √(1 - GM/(c2・r))・・・・⑯
が得られる。
なぜか、式⑨では、2GM となるところが、式⑯では、GM になっている。
もともと万有引力の法則など一般相対性理論以外の方程式は、一般相対性理論においては、相対速度が光速度 c よりも十分に小さい場合で、重力加速度(加速度)が十分に小さいときに近似になりたつ法則なので、それを一般相対性理論の計算に利用しようとしている点に無理があるのだと思うが、、違いが発生した原因はよくわからない。
シュバルツシルト解についての解説本等を見る限りは、今回の答えの方が正しいらしい。
次に、長さについて検討する。
特殊相対性理論では、観測者と相対速度 v で移動するロケットの内部での長さ X' が、観測者から長さ X と観測されるとすると、ローレンツ収縮により式⑭のβにより
X = β・X'
と、縮小して観測される。
実は、私自身今回もつまずいたが、どうもローレンツ縮小、ローレンツ変換はどちらからみて、時間と長さがどのように変換されるのか、勘違いしそうになるので、もう一度整理しておくと、
観測者から観測するロケット内部の時間を T、ロケット内部の長さを X
ロケット内部で観測される時間を T'、長さを X' とすると、
T' = β・T・・・・⑰
X' = (1/β)・X・・・・⑱
となる。
つまり、観測者の観測する時間で、10年、ロケット内部の長さ 1m は、
ロケット内部では、時間 1年、長さ 10m となる。
時間と、長さの拡大・縮小の関係が逆になっているのだが、いつも忘れて勘違いしそうになる。
特殊相対性理論のおさらいはこれぐらいにして、次に、長さの歪がどうなるか検討してみる。
シュバルツシルト解においては、時空の歪が式⑰で得られ、時間は特殊相対性理論と同様に式⑰で得られることがわかった。
では長さは特殊相対性理論と同様に、式⑱で得られるのだろうか?
時空の歪を図にしてみた。

実線の円を中心の質量 M の星とする。
その星から距離 r の位置に質量 m のロケットがあるとする。
ロケットから観測される時空の歪 β は、式⑯から計算できる。
距離 r の位置での時空の歪の半径を R とする。
半径 R は、 時間軸(T)、空間軸 (X、Y、Z) のどの座標とも違う、別の空間軸 (仮にWとする) の方向の値。
3次元空間にいる我々からは W 軸は時空の歪としてしか認識できない。
この座標軸は実在するのかと疑問になるが、その問題についてはまた後日検討する。
距離 r と、R は質量 M の星の重力の影響を受けない無限遠から観測した長さであることに注意。
これを混同すると訳が分からなくなる。(私自身、混同して訳が分からなくなった。)
ロケット M から観測する質量 M の星の中心までの距離を r' とすると、r' は r よりも長くなる。
このようになる理由を図で説明する。
ロケット M は図の点線で示す半径 R の球体(巨大な星と思ってもよい。)の地表面にあると考えると、
地表面にロケットから計測して距離 r' 離れた位置に、質量 M の中心があることになる。
地表面はかった距離 r' は円弧の長さになるので、 直線で計測した長さ r よりも長くなる。
時空の歪みβを、r と、r' で表すと
β = r / r' ・・・・⑲
無限遠から観測した半径 r から、ロケット m が観測する半径 r' を求めると、
r' = (1/β) r ・・・・⑳
となり、
特殊相対性理論において、時空の歪がβである場合の以下の式⑱と同じになることが分かった。
X' = (1/β)・X ・・・・⑱
以上より、シュバルツシルト解における時空の歪が計算できたので、時空の距離 ds2 を計算してみる。
ロケット m から観測する時空の距離 ds は、ロケットから観測される時間 T' と、長さ X' により、
ds2 = - cT'2 + X'2 ・・・・(21)
となる。
これに、式⑰と、⑱を代入すると、
T' = β・T ・・・・⑰
X' = (1/β)・X ・・・・⑱
ds2 = - β(c・T) 2 + ((1/β) X) 2 ・・・・(22)
となり、シュバルツシルト解における時空の距離の計算式⑧が得られた。
今回の目的は達成できたが、実際の時空の歪についてもう少し検討してみる。
質量 M の星の中心と、半径 R の球体の中心 O と、質量 m のロケットのなす角度を θ (ラジアン)とすると、
θ = r' / R ・・・・(23)
r = R・sin(θ) ・・・・(24)
を、⑲ に代入すると、
β = R・sin(θ) / r' となるので、これに式(23)を代入すると、
β = sin(θ) / θ ・・・・(25)
となる。
また、式(24)より
R = r / sin(θ) ・・・・(26)
が得られる。
実際に地球の地表面付近での、時空の歪 β 、θ、 半径 r、半径 R' を求めてみる。
計算には以下の値を使った。
万有引力定数 G = 6.67384×10-11 m3 / kg・s2
地球の質量 M = 5.972×1024 kg
光速度 c = 3.0×108 m
地球の中心からの半径 r' = 6.371 × 106 m
まず、時空の歪みβは、式⑨に、G、M、c、r を代入すると求められる。
本来は無限遠から観測した半径 r を使うべきだが、わからないので、 r には、r' を代入する。
後で計算するが、r と、r' の差はごくわずかなので、近似的には問題ない。
β = √(1 - 2GM/(c2・r))・・・・⑨
β = 0.999999999304903
求めた β から、無限遠から観測した半径 r を求めてみる。
β = r / r' ・・・・⑲
より、
r = 6,370,999. 996 m
r' との差はわずか 4mm しかない。
もともと r の近似値として r' を使ったが、問題なかったことがお分かり頂けると思う。
地球の半径 6,371km が一般相対性理論による影響で、わずか 4mm ちじむだけなので、
おそらく現在の技術では地球上で時空の歪み β を測定するのはほとんど不可能だと思われる。
次に、β と、r から時空の歪によって発生する重力加速度 g を計算してみる。
わずか 4mm の歪が、地表面での重力加速度 9.8 m / s2 の原因だと考えるとホントかなと思うが、
「一般相対性理論 重力は時空の歪により発生する 」で時空の歪と r から g を計算する式(27)を求めているので、
g = (1 - β2)・c2 / r ・・・・(27)
これに、β、c、r を代入すると、
g = 19.6385931 m/s2
あれれ、、g = 9.8 m/s2 の2倍になってしまった。
そうか、式(27)は、もともと式⑮を g が左辺にくるようにしたものだったが、
β = √(1 - gr/c2)・・・・⑮
式⑮から求めた式⑯は、
β= √(1 - GM/(c2・r))・・・・⑯
今回使った式、⑨と比較すると gr の部分が 2 倍になっているので、結果 g も2倍になっている。
β= √(1 - 2GM/(c2・r))・・・・⑨
つまり、今回使った式⑨の場合、式(27)は、式(28)に修正しなければならない。
g = (1 - β2)・c2 / (2・r) ・・・・(28)
これに、β、c、r を代入すると、
g = 9.8192965 m/s2
となり、地球の地表での重力加速度 g = 9.8 m/s2 に近い値が求まった。
次に、θ を求めてみる。
β = sin(θ) / θ ・・・・(25)
に、β を代入して、θ を計算すると、(特別な逆関数がいるので、EXCEL VBA で関数を定義して計算した。)
θ = 0.000064580030968 ラジアン
これを、秒(1/3,600度)に変換すると
θ = 13.32秒
と微小な角度だが、高性能な天体望遠鏡であれば十分観測できる角度である。
たとえば、「すばる望遠鏡」の分解能は、0.2 秒角 である。
実際には、X、Y、Z の空間の座標軸のどれでもない、座標軸 W 方向の角度を測定する方法などないので、、実現の方法は無い。
時空の歪みを測定するには、やはり β = r / r' ・・・・⑲ の関係と、重力の方向と垂直の方向(つまり円周方向)には長さが歪まないことから、
円周の長さ 2πr を実測してもとめた r と、実測して求めた r' を式⑲に代入して β を求めるしかなさそうだ。
ただし、r と、 r' の差が地球の地表面の場合では 4mm しかないので、やはり、実測はきわめて厳しいと思われる。
最後に、R を求めてみる。
θ = r' / R ・・・・(23) に、r' と θを代入すると、
R = 9.865×1010 m
となる。
この半径は、おおよそ太陽から金星までの距離 10.820 × 1010 m に近い値である。
つまり、地球の地表付近の地球の重力による時空の歪は、太陽を中心として金星までの距離を半径とする巨大な球体の表面の歪に相当する。
この値を求めてみて、最初、私自身は時空の歪を示す球体の大きさが、以外と小さいと感じた。
光は時空の歪に沿って進むので、地球から発した光は地球の重力の影響で、地球の太陽の周回軌道よりも大きな曲りで曲がる様に思えてしまう。
そんなことは、ないだろ、、と思って少し考えると直ぐ分った。
重力の影響による時空の歪は、重力の中心からの距離 r によって変わるので、地球からの距離 r が離れると R の値も大きくなる。
このため、地球から出た光が太陽の周りを一周してしまうことはない。
実際に、地球の中心からの距離 r と、R の関係をグラフにしてみた。
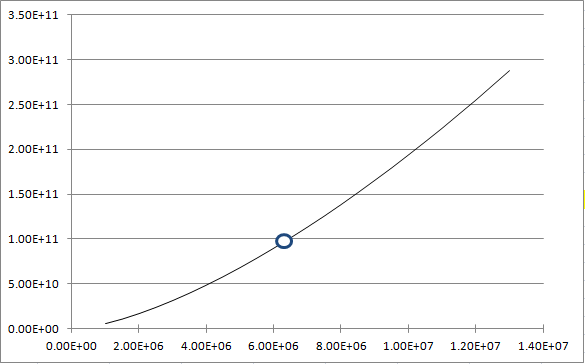
青い丸が地球の地表面の位置 r での時空の歪の半径 R である。
地球の中心からの距離 r が、2 倍になると、時空の歪の半径 R は 2 倍以上になる。
地球の中心からの距離が離れると、時空の歪の半径 R は急速に大きくなり、地球の重力の影響を受けない無限大の距離では、時空の歪の半径も無限大になり、時空は歪がなく平坦になる。
今回のまとめ
アインシュタインの重力方程式の解の1つ「シュヴァルツシルトの解」の外部解における時空の距離 ds2は、以下の通り。
ds2 = -(β・c・dt)2 + ((1/β)・dx)2・・・・⑧
シュバルツシルト解の初期条件(境界条件)で、時空の歪は星の中心から球対象であるとしたので、半径方向を x 軸にとり、y軸と、z軸は 0 とした。
β: 質量 M の星の中心から半径 r の位置の時空の歪で、以下の通り。
β= √(1 - 2GM/(c2・r))・・・・⑨
G: 万有引力定数
c: 光速度
dx: 星の中心を 0 とした場合の半径 r 方向の座標
r: 星の重力の影響を受けない無限遠から観測した半径
重力の中心からの距離 r と、その位置での時空の歪 β から、その位置での重力 g を計算すると、以下の通り。
g = (1 - β2)・c2 / (2・r) ・・・・(28)
重力 g の方向は、半径 r の方向。
星の重力の影響を受けない無縁縁遠から観測した、半径 r の位置での時間を T、長さを X から、
半径 r の位置で観測される時間を T'、長さを X' を求めると以下の通り。
T' = β・T ・・・・⑰
X' = (1/β)・X ・・・・⑱
距離 r の位置での時空(X, Y, Z) とは別の空間軸 W 方向の時空の歪の半径を R 、
質量 M の星の中心と、半径 R の球体の中心 O と、質量 m のロケットのなす角度を θ (ラジアン)とすると、
β = sin(θ) / θ ・・・・(25)
θ = r' / R ・・・・(23)
式(25)から、θ が求まり、式(23)に代入すると、R が求まる。
Rは、r (r') の関数で、r(r') が増加すると、R も増加する。
実際の計算例
地球の重力による時空の歪について実際に求めてみた。
万有引力定数 G = 6.67384×10-11 m3 / kg・s2
地球の質量 M = 5.972×1024 kg
光速度 c = 3.0×108 m
地球の中心からの半径 r' = 6.371 × 106 m
とすると、地球の地表面付近での値は以下の通り、
β = 0.999999999304903
r = 6,370,999. 996 m (r' との差はわずか 4mm)
g = 9.8192965 m/s2
θ = 0.000064580030968 ラジアン = 13.32秒
R = 9.865×1010 m (おおよそ太陽から金星までの距離 10.820 × 1010 m に近い値)
次回は、地球よりもずっと質量の大きな星の場合について考えてみる。
つまり、ブラックホールについて検討する。
 SalesWeb は、インターネットでお客様と、当社のサーバを結び、販売管理・在庫管理・運賃管理・保管料荷役料管理の機能を提供するクラウドサービスです。
http://www.salesweb.jp
SalesWeb は、インターネットでお客様と、当社のサーバを結び、販売管理・在庫管理・運賃管理・保管料荷役料管理の機能を提供するクラウドサービスです。
http://www.salesweb.jp
